极限和无穷大
当 x 趋近无穷大时,这个函数的极限是什么?
若 "x" 越来越大,"2x" 也越来越大:
| x | y=2x |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 4 | 8 |
| 10 | 20 |
| 100 | 200 |
| ... | ... |
所以当 "x" 趋近无穷大时,"2x" 也趋近无穷大。我们这样写:
💡
不要被这个 "="号迷惑了!我们其实无法达到无穷大,但在 "极限" 的语言里,极限是无穷大 。
无穷大和次方
实际上,很多无穷大的极限是很容易求的,只要我们知道函数的 "走势",像这样
- 当 x 趋近无穷大时,像 1/x 的函数趋近 0 。像 1/x2 等的函数也一样。
- 像 x 的函数会趋近无穷大,2x 或 x/9 等函数也一样。同样,含有 x2 或 x3 等的函数也会趋近无穷大。
- 但要小心,函数 "−x" 趋近 "负无穷大",所以我们要留意 x 的正负号。
例子: 2x2−5x
- 2x2 趋近 +无穷大
- −5x 趋近 −无穷大
- 但 x2 增加得比 x 快,所以 2x2−5x 会趋近 +无穷大
如果我们留意函数的 次方数 (函数里最高的 指数),我们便可以知道答案:
如果函数的次数是:
- 大于 0,极限是无穷大(或 −无穷大)
- 小于 0,极限是0
但是,如果次方数是 0 或未知值,情形便会复杂一点。
有理函数的次方
有理函数 是两个多项式的比:$$f(x)=\frac{P(x)}{Q(x)}$$
例如,在这里: $$ \frac{P(x)}{Q(x)} = \frac{x^3 + 2x - 1}{6x^2} $$
根据上面 方程的次方数 概念,求极限的第一步是……
比较 P(x) 和 Q(x) 的次数:
- 如果 P 的次数小于 Q 的次数:则极限是0
- 如果 P 的次数等于 Q 的次数:用最高指数的项的系数相除,像这样:$$\lim_{x\to ∞}\frac{5x^2 + 1} {3x^2 - x} = \frac{5}{3} $$
- 如果 P 的次数大于 Q 的次数:极限是正无穷大,或负无穷大。不要忘了看正负号!要确定极限是正还是负,我们看有最大指数的项的正负号,好像在上面找系数一样:$$\frac{x^3 + 2x - 1}{6x^2}$$ 上面有最大指数的项 和 下面有最大指数的项 都有正号; $$\frac{-2x^2 + x}{5x - 3} = \frac{-2}{5}$$ 这个函数的极限是负无穷大,因为 -2/5 是负数。
求 "e"
有一个 e (欧拉数) 的公式是基于无穷大和这个公式的:
所以我们不求 "取无穷大" 的值,我们尝试用越来越大的 n值:
| n | (1 + 1/n)^n |
|---|---|
| 1 | 2.00000 |
| 2 | 2.25000 |
| 5 | 2.48832 |
| 10 | 2.59374 |
| 100 | 2.70481 |
| 1,000 | 2.71692 |
| 10,000 | 2.71815 |
| 100,000 | 2.71827 |
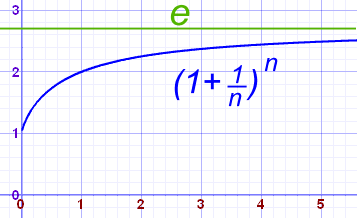
结果趋近 2.71828...,这就是 e (欧拉数) 的值。
我们又看到这个现象了:
- 我们不知道函数在 n=无穷大 的值
- 但我们看到结果趋近 2.71828……
因此,我们用极限来表达答案:
当 n 越来越大时,答案便越来越接近 e
不要犯错 …… !
我们看到当 n 越来越大时,函数趋近 2.71828……
但如果我们想把无穷大当作一个 "很大的实数" (它不是!),我们会得到:
(1+1/∞)∞ = (1+0)∞ = (1)∞ = 1 (大错特错!)
所以,不要把无穷大当作一个实数:你会得到错误的答案!
极限才是正途。
无穷大的特别属性
| 无穷大的特别属性 |
|---|
| ∞ + ∞ = ∞ |
| -∞ + -∞ = -∞ |
| ∞ × ∞ = ∞ |
| -∞ × -∞ = ∞ |
| -∞ × ∞ = -∞ |
| x + ∞ = ∞ |
| x + (-∞) = -∞ |
| x - ∞ = -∞ |
| x - (-∞) = ∞ |
| 如果 x>0 : |
| x × ∞ = ∞ |
| x × (-∞) = -∞ |
| 如果 x<0 : |
| x × ∞ = -∞ |
| x × (-∞) = ∞ |
未定义运算
以下的运算都是"未定义的":
| "未定义"运算 |
|---|
| 0 × ∞ |
| 0 × -∞ |
| ∞ + -∞ |
| ∞ - ∞ |
| ∞ / ∞ |
| ∞^0 |
| 1^∞ |
例子:∞ / ∞ 是不是等于 1?
不是,因为我们不知道无穷大有多大,所以我们不能说两个无穷大是一样的。
例如,∞ + ∞ = ∞,所以
$$ \frac{∞}{∞} = \frac{∞+∞}{∞} $$ 即 $$\frac{1}{1}=\frac{2}{1}$$
所以这是错的,∞ / ∞ 不等于 1 ,它是未定义的。
不是,因为我们不知道无穷大有多大,所以我们不能说两个无穷大是一样的。
例如,∞ + ∞ = ∞,所以
$$ \frac{∞}{∞} = \frac{∞+∞}{∞} $$ 即 $$\frac{1}{1}=\frac{2}{1}$$
所以这是错的,∞ / ∞ 不等于 1 ,它是未定义的。