微积分入门
微积分一词"Calculus"源自拉丁语,意思是"小石头",它从分析小的部分来了解大的整体。
- 微分是把整体分拆为小部分来求它怎样改变。
- 积分是把小部分连接(积)在一起来求整体有多大。
微积分完全是关于 改变 的学问,看下面的对场景。
汽车瞬时速度问题
小山和小李开车去出旅行……但车速表坏了。
小李: | "小山!我们现在开得多快?" |
小山: | "等一等……" "上一分钟我们走了 1.2 千米,所以车速是:" 1.2 千米m/分钟 × 一小时 60 分钟 = 每小时 72 千米 |
小李: | "不,小山! 我不是问上一分钟或上一秒的平均速度,我想知道我们现在的速度。" |
小山: | "那么我们在这里测量……这个路标……来!" "好了,我们在路标待了零秒,走了……零米!" 速度是 0米 / 0秒 = 0/0 = 我不知道是多少! "小李,我没招了!我要知道在某个时间里走的某个距离,才能计算速度。但你说时间是零?不可能!" |
那……可不可以求一个相当准确的近似值?
自由落体瞬时速度
我们这个故事还没结束呢!
到达目的地,小山和小李终于可以下车了。憋在车里几个小时后,小山想伸展一下筋骨。
他是个跑酷高手,所以他要做一个高难度动作:小山会从 20m 高的房屋上跳下来。小李是个摄影师,他问:"起跳一秒后你会下落得多快?"
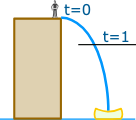
小山用这个简单的公式来计算已经落下的距离:
- d = 跌了的距离(米)
- t = 起跳后的时间(秒)
(注意:这个公式是从物体在 引力 影响下,下落距离的公式:d = ½gt2 简化而成的。)
那是多快?速度是距离除以时间:
1秒后:
"可是",小李说,"这也是从你起跳开始的平均速度,…… 我想知道的是刚好在 1秒时的速度,好让我准备好我的相机。"
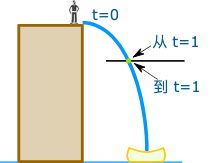
小山又没招了。
距离是多少?时差是多少?
两者都是零,根本不可能计算!
小山有个想法 …… 用很短的时差,短到对答案没什么影响。
小山不会去求这个时差的值,他只给它一个名字:"Δt" (叫 "delta t")。
接下来,小山算出从 t 到 t+Δt 的时间里他落下的距离
在(1+Δt) 秒,小山落下了:$$d=5t^2=5x(1+Δt)^2$$
展开 $$(1+Δt)^2=(1+Δt)(1+Δt)=1+2Δt+(Δt)^2$$
结果是:$$d=5x(1+2Δt+(Δt)^2)=5+10Δt+5(Δt)^2$$
所以在 1秒 到 (1+Δt) 秒这段时间里,他落下的距离是:
$$d的改变=(5+10Δt+5(Δt)^2)−5米$$ $$=10Δt+5(Δt)^2米$$
现在用这个距离除以时间来求速度:
$$速率=\frac{10Δt+5(Δt)^2米}{Δt秒}$$ $$=10+5Δt 米每秒$$
所以速度是 10 + 5Δt m/s,小山想 …… "这 Δt …… 要越短越好 …… 所以就干脆把它变成零不就行了吗?这样结果便是:
速度 = 10米每秒
厉害!小山得到答案了!
小山:"我下跌1秒后的速度正好是 10 m/s"
小李:"你刚才不是说你不能计算这个速度吗?"
小山:"刚才我还没用微积分!"
微积分
的确,他是用了微积分。小山用 微分 把时间和距离切成小块来求精确的答案。
小山的算法是不是个巧合?可以用来解其他的问题吗?
我们用这个函数 y = x3 来试试
这个例子和上面的很相似,但只不过是个图的坡度,并不需要从屋顶跳下来!
在 x = 1, $$y = 1^3 = 1$$
在 x = (1+Δx), $$y = (1+Δx)^3$$
展开$$ (1+Δx)^3 $$为$$ 1 + 3Δx + 3(Δx)^2 + (Δx)^3$$,得到:
$$y = 1 + 3Δx + 3(Δx)^2 + (Δx)^3$$
y 从 x = 1 到 x = 1+Δx 的差值是:
$$y 的改变 = 1 + 3Δx + 3(Δx)^2 + (Δx)^3 − 1$$
$$= 3Δx + 3(Δx)^2 + (Δx)^3$$
我们可以求坡度了:
$$坡度 = \frac{3Δx + 3(Δx)^2 + (Δx)^3}{Δx} = 3 + 3Δx + (Δx)^2$$
和上面一样,Δx 缩小到零,剩下:
坡度 = 3
这是$$ y = x^3$$ 的图
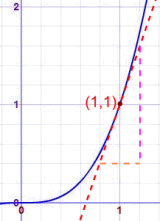
坡度持续地改变,但在 (1,1) 这点,我们可以画一条切线,然后算出在那一点的坡度是等于 3的(你可以数数格子来看看!)
结论
微积分是关于改变的。
微分把整体分拆为小部分来求它怎样改变。
- 你可以在 导数入门 学习更多内容
积分把小部分连接(积)在一起来求整体有多大。
- 你可以在 积分入门 学习更多内容