极限

极限求值

有时我们不能直接计算一个事物的值……可是我们可以去看看越来越接近它时的情形，详细内容见极限入门。

"求值" 的意思是计算……的值

在上面的例子里，极限是 2，因为函数趋近 2。但这样说是不够的！

其实有很多方法去求精确的答案。我们来看看其中几个：

一. 带入变量的值

首先要尝试的方法是代入变量的值，来看看可不可以直接算出答案（换句话说，代换）。试试一些例子：

$$ \lim_{x\to 1} \frac{x^2 - 1}{x -1} = (1-1)/(1-1) = 0/0 $$ ：不可行。
$$ \lim_{x\to 10} \frac{x}{2} = 10/2 = 5 $$ ：可行。

在第一个例子里，代换法不管用，但在第二个例子里我们很容易得到答案。

我们可以尝试因式分解。

因式分解 $$(x^2−1)$$ 为 (x−1)(x+1)，我们得到：

$$ \lim_{x\to 1}\frac{x^2-1}{x-1}=\lim_{x\to 1}\frac{(x-1)(x+1)}{x -1}=\lim_{x\to 1}(x+1)$$

我们现在可以代入 x=1 来求极限：

$$ \lim_{x\to 1}(x+1) = 1+1 = 2 $$

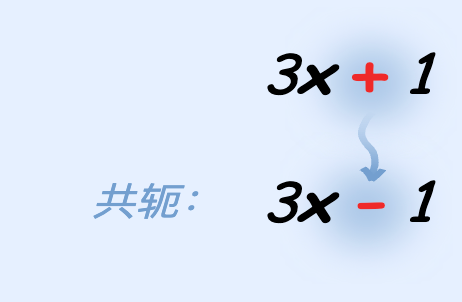
若函数是个分数，把上面和下面乘以共轭可能会有帮助。共轭是把

把两个项之间的正负号倒转：